Probabilistic data structures create beautiful connections between mathematics and computer science. Bloom filters are perhaps the best-known example - they use multiple hash functions and probability theory to test set membership with minimal memory usage.

While most software engineers are familiar with basic Bloom filters, fewer know about their variants which often contain equally elegant insights. In this post, I'll introduce Counting Bloom filters and explore how a 2012 paper (PDF) used arithmetic properties to optimize their memory usage. Instead of incrementing the count fields by 1, they showed how carefully chosen increment values could encode counting state in the properties of addition itself.

Let's look at how this works.

The Original Bloom Filter

A Bloom filter is an elegant probabilistic data structure that tests whether an element is in a set. It uses k hash functions to map each element to k positions in a bit array, setting those bits to 1. To test membership, we check if all k bits for an element are 1.

The tradeoff is allowing false positives (saying an element is present when it isn't) in exchange for space-efficiency. But there's another limitation - you can't delete elements because you don't know if other elements also set those bits.

Element x    Element y
   ↓   ↓     ↓   ↓  
[0 1 0 1 0 0 1 0 1 0]

Adding Counting with CBF

The Counting Bloom Filter (CBF) solves the deletion problem by replacing each bit with a small counter. When adding an element, increment its k counters by 1. To delete, decrement them.

The cost? Memory usage. With 4-bit counters and 1% false positive rate, CBF requires ~40 bits per element - about 4x the memory of an equivalent Bloom Filter.

Element x    Element y
 +1↓ +1↓   +1↓ +1↓
[0 1 0 2 0 0 3 0 1 0]

A good example use case for CBF is distributed caching. Each cache node maintains a CBF of its contents, allowing it to track insertions and deletions locally. It can then collapse its CBF into a standard Bloom filter by setting bits where counters are positive. These compressed filters can then be efficiently shared across the network to help route cache requests to the right node. The CBF enables this dynamic cache routing while still supporting item eviction - something impossible with standard Bloom filters.

Enter Bh Sequences

Here's where number theory comes in. A Bh sequence is a set of integers where all sums of h or fewer elements are unique. For example, with h=2, you might need numbers like {1,22,55,72} where no sum of two numbers from the set equals any other sum:

1  + 1  = 2
1  + 22 = 23
1  + 55 = 56
1  + 72 = 73
22 + 22 = 44
22 + 55 = 77
22 + 72 = 94
55 + 55 = 110
55 + 72 = 127
72 + 72 = 144

This property means that given a sum, you can determine which numbers from the sequence were added together to produce it.

The Bh-Counting Bloom Filter

The first optimization combines CBFs with Bh sequences. Each array position now has two counters:

1. A regular counter tracking the number of elements (like CBF)
2. A weighted sum using values from a Bh sequence as increments

             Element x   Element y
               +1↓ +1↓    +1↓ +1↓
Counter:      [0 1 0 2 0 0  3 0 1 0]
               +4↓ +5↓    +7↓ +5↓
Weighted Sum: [0 4 0 9 0 0 16 0 5 0]

The Bh sequence property lets us detect false positives more accurately - if an element's increment values couldn't have contributed to the weighted sums we see, it can't be in the set.

The Final Form: VI-CBF

The Variable-Increment CBF optimizes the Bh-CBF by eliminating the counter field:

             Element x   Element y
               +4↓ +5↓    +7↓ +5↓
Weighted Sum: [0 4 0 9 0 0 16 0 5 0]

This reduces memory usage by half at the cost of an increased false positive rate due to how the query function uses the weighted sum to determine if an element does not belong to the set.

The paper uses a simple and elegant sequence D_L = [L, 2L-1] = {L, L+1,...,2L-1} as the increment set where L is the size of the set and must be a power of 2. For example, with L=4, increments are chosen from D₄ = {4,5,6,7}. This choice has a key property: any number between 2L and 3L-1 is a sum of exactly 2 values from D_L. So when querying an element z that maps to increment v, based on the value of the weighted sum c for each position, we can use these rules to determine whether z might be in the set:

• If c = 0: z definitely isn't in the set
• If 1 < c < L: z definitely isn't in the set
• If L < c < 2L: c must be a single increment value; if c ≠ v, z isn't in the set
• If 2L ≤ c < 3L: c must be a sum of two increments; VI-CBF checks if v could be part of such a sum
• If c ≥ 3L: the sum provides no useful information

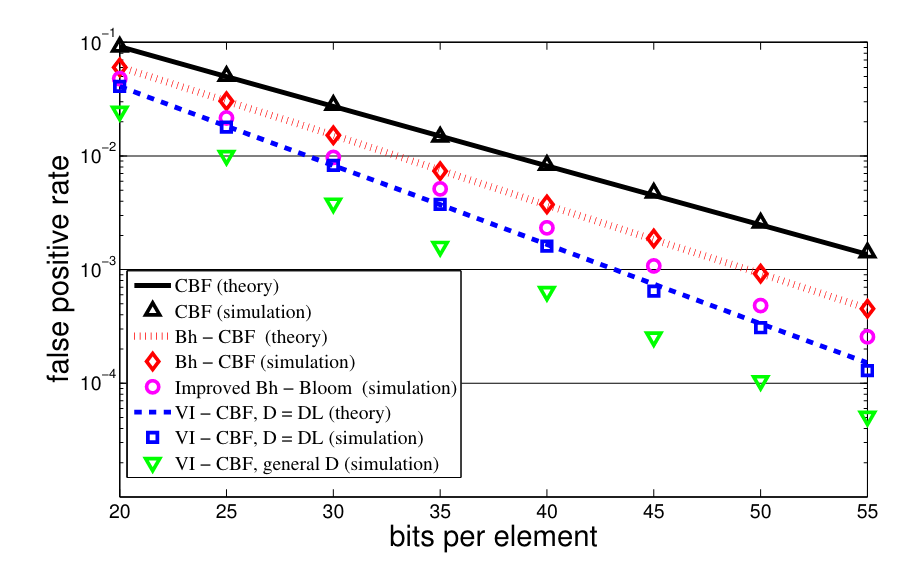
On net, the benchmarks in the paper found a ~1/3 reduction in memory usage overall for the VI-CBF compared to the CBF:

Conclusion

Probabilistic data structures such as bloom filters help us make powerful space/accuracy tradeoffs in computer systems. VI-CBF shows us something even more interesting - how arithmetic properties can replace explicit state tracking, leading to simpler and more efficient implementations. There are many more possibilities than just the basic bloom filter and I hope learning about the VI-CBF piqued your curiosity to explore these more.

You can find the full paper here:

• ACM Digital Library Record
• PDF